 |
 |
|||
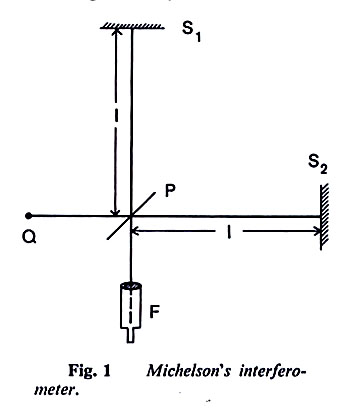
| What a vacuum really is is a matter of debate. | This 1880 experiment looked for ether but found none. |
back to Stopdown, home page, click here
back to Stopdown/science, home page, click here
Special Relativity
 |
 |
|||
| What a vacuum really is is a matter of debate. | This 1880 experiment looked for ether but found none. |
In the late 1800's physicists believed that light, being a wave form, had to have a medium to travel in, like sound waves which require air, water or some material medium in order to "propagate" ( to travel). The presumed medium for light waves in space, starlight, was called ether. Physical objects, like the earth, were supposed to pass through the ether and the ether through them without any disturbance. The trouble was the ether could not be detected by experiments. The device above, perhaps the most famous experimental device in all of physics, attempted to look at interference changes that one would expect upon rotation of the device if light did travel via the supposed medium called ether. No changes in interference appeared as expected when the device was rotated. Scientists came up with arguments around the experimental facts that might salvage the ether, but nothing convincing fell into place.
Albert Einstein's theory of "special relativity," published in 1905, claimed, for one thing, that there was no ether -- starlight traveled in a vacuum, that is, in empty space. (James Maxwell, who came up with the equations for electromagnetic radiation (light), had not based his thinking on the existence of any medium for light) But if there was no medium, no "ether", to be the reference frame, as with sound traveling at a fixed velocity with respect to the reference frame of air, then what determined the speed of light when the light source and observer were moving with respect to each other? If a light source moves toward an observer at 100 miles an hour would the light have a higher velocity, as it reached the observer, than if the light source and the observer were stationary (not moving) with respect to each other? Is this any different from the observer moving towards the light source? Likewise, if the light source and observer are moving away from each other, would the light be slowed down in the observer's perception, and does it matter which one we say is moving or stationary? What Einstein claimed is that all observers in space will measure incoming light as having the same velocity, no matter what the motion of the source of the light, and no matter what the motion of the observer, and that velocity of light is independent of the velocity of the source of the light. As shown by the figures below, this doesn't make sense by normal thinking.
.
"The speed of light is constant in all moving frames of reference"....illustration of the concept.
In figure 1 below, observer 1 and observer 2 -- O1 and O2 -- are on platforms in space. As shown by arrows, O1 is moving towards the light source, and O2 is moving away from the light source. O1's light meters, marked m, span the same distance as O2's light meters. According to Einstein's theory of special relativity the the observers O1 and O2 will get the same measurement for the velocity of the light pulse, as measured by the time the pulse takes to pass from the first to the second meter (sensor)....... If we call the red arrow a bullet in space instead of a flash of light, we would expect O1and O2 to get different measurements for the bullet's velocity because of their own velocities toward and away from the bullet. Normal mathematical thinking on comparative velocities can be shown by the example of a train and a car, moving parallel to each other. If you are in a car traveling at 30 miles per hour, and a train is moving along side you in the same direction at 50 miles per hour, the train will pass you at a relative speed of 20 miles per hour. (50 - 30 = 20) If, on the other hand, the train is moving along side you but in the opposite direction, its speed relative to you will be 80 miles per hour. (50 + 30 = 80) With light, according to special relativity, common sense about relative velocities does not apply. (In fact, according to special relativity, the relative motion of the train and the car deviate from standard math at very high velocities.
| figure 1: A pulse of light moves towards two observers, one moving towards the light source, the other moving away from it. |
In the figure 2 below, the light sources are on platforms moving toward and away from an observer O, whose platform has two light meters. According to special relativity, the light pulses from the two sources will be found to have the same velocity. If projectiles such as bullets, were fired from these moving platforms, they would pass the observer at different velocities, assuming we are in space and there is no air to slow the projectiles. If the bullets are fired with the same velocity from their source platforms, the platform moving towards O would be expected to impart extra velocity to the bullet, as measured in O's frame. The platform moving away from O would be expected to decrease the speed of the bullet, as perceived by O. With light, according to special relativity, this logic does not apply. A binary star system, which is two stars rotating around each other like two ice skaters holding hands, gives an example of this situation in nature. (Click here for discussion of binary star, or scroll down.)
|
figure 2. One light source is moving towards observer O, the other light source is moving away from O. According to Special Relativity pulses of light from these sources will reach O with the same velocity, as measured by the light meters on O's platform. |
|||
| figure 2a. The light source on the left is moving towards the observer, O, the light source on the right is moving away. |
Note: There was an article in the New York Times, about two years ago, about a girl who is taking PhD level courses in physics at 13 years old. Her professors say her grasp of the material is deep, and she doesn't take notes. (She read at less than two years old and finished high school something like 9 or 10 years old.) She told the reporter she was interested in arguments against Einstein's claim that the speed of light is constant in all moving frames of reference, and intended to pursue inquiries in that vein.
Einstein's remake of the concept that two events are simultaneous -- that two events happen at the same time.
In figure 3, below observer O' (0 "prime") is on a train moving past O on the platform. The flashes of light are on the platform, and will reach O at the same time because he is at the mid-point. But O' will move to the right so he will see the right flash before the left. We would normally say that the flashes are simultaneous, because their signals will reach a midpoint at the same time, and that this fact holds true for O and O', even if it does not appear to be the case in the frame of reference of O'. Special relativity says that there is no "privileged" frame that all observers can call the true frame. The observer on the train sees the flashes on the platform at different times, this means that the flashes are not simultaneous in his frame, and, (here's the twist) his frame is just as valid as the platform frame. Another example: Let's suppose in figure 3 the left flash is emitted before the right flash (on the platform) and O' moves to the right such that O' sees the flashes at the same time. O, on the platform, sees them at different times. Now the usual way to look at this is to say the flashes are not simultaneous, and that O, at the midpoint, is correct in this perception. The flashes appear simultaneous to O', but this is an illusion created by his motion, we would normally say. Special relativity says that they are both right, in their own frame, and that the perception of O' that the flashes are simultaneous is just as valid and the the perception of O that they are not.
| figure 3 .......O' is on a train, moving to the right, relative to O, who is on the platform . The flashes occur on the platform. O sees them at the same time. O' sees right flash before the left. |
Usually we think of distance and time as pure measures on whose terms the events of matter and energy are played out. Whether you are close to a tree or far away, the height of the tree is a measurable reality. What Relativity does is put light ahead of distance and time as the basis of measurements in the universe. Distance and time depend on the observer, but the speed of light is constant for all observers.
................................................................
Note: It is important, when studying relativity, to remember that when there are two moving frames, and neither is accelerating, it doesn't matter which frame we say is moving and which we say is not moving. What matters is the relative velocity, and this is basic physics, not special relativity physics. For instance in figure 3 above, we can say O' is moving past O. Or we can say O (and the platform and ground) is moving to the left and O' is not moving. Or we can say they are both moving. These are different descriptions of the same physical event. In these stiuations the relative velocity is the same, and it is the defining measurement. In the figure below the upper and lower image describe the same situation, (if the arrows represent constant velocity, not acceleration).
Comparing figure 3 and figure 4, here is a question we would like to ask, bases on the the stars in figure 4 being light sources. If O' in figure 3 sees the right flash before the left, then so will O - the observer, in figure 4. These are identical situations. But if the the top and bottom pictures below represent the same physical situation (without acceleration) then the observer will see the right flash before the left, whether his situation is depicted as in the top or bottom frame. Going back to figure 2a, we see the same situation, but in that case we said that the observer measures the incoming light as having the same speed. (Because that's what Special Relativity says must be the case.) So in both the top and bottom images in figure 4, the observer will see the right flash before the left. But if he is equipped with light meters as in 2a, he will measure the speed as the same. So, flashes are emitted at the same distance from the observer, who sees one flash before the other even though they arrive at the same velocity. We would like to receive commentary on this analysis, as to its correctness, and comments on the meaning of this contradiction, if the analysis is correct.
figure 4
Note: It is important to understand the difference between an inertial frame and an accelerating frame. This distinction was first recognized by Isaac Newton............The meaning of inertia is that if a rocket is moving, with its rocket motors turned off, at a constant velocity in space, it will continue at the same velocity and in the same direction so long as its rocket motors are off (and so long as it stays outside any gravitational field.) It does not slow down because there is nothing to slow it down, it just keeps going. A cloud of dust may slow it down, or a the ship's rocket motors can cause a change, but unless something exerts a force on it it just keeps going. What keeps this from happening with a projectile (i.e. a ball thrown in the air) on earth is air and other sources of friction, as well as gravity. People on the spaceship, when it is moving at a constant velocity, will feel no effects from the motion of the ship. Motion at a constant velocity, for an object in space, is no different from standing still, in terms of the physical state of the object, whose state is called is called an inertial frame. When force is applied, like firing a rocket, the object (frame) accelerates (its velocity increases) as long as the force is applied, and the object is no longer an inertial frame -- it is an accelerated frame. People in the rocket will feel a constant force if the rocket accelerates at a constant rate, such as gaining 5 miles per hour in velocity every 10 seconds, just like someone in an accelerating car is pressed back against the seat. As soon as the rocket motor stops the ship stops accelerating and becomes an inertial frame once again. Again the people in the rocket feel no force of motion, but feel that they are standing still. Likewise n a car a passenger, when the car is traveling at a constant velocity, is not pressed back against the seat as when accelerating.
............................................................................................................................................................................................................................
It may be worthwhile to take a step back and consider how light velocities would be interpreted with the medium of the "ether" as a reality. Consider how sound waves are effected by relative motion. If an ambulance is moving towards an observer by the side of the road, the sound waves from the siren will compress in the air and travel at the speed of sound in air, but with a higher pitch because of the compression from the ambulance's motion (the "Doppler effect", see graphic below.) If, on the other hand, the siren is stationary and the observer is moving toward it in a car, the pitch will be higher, but in this case the higher pitch is due to the sound reaching the observer faster than the speed of sound in air, because of the movement of the car through the air. Now if there were "ether" and the light waves moved in that medium as sound moves in air, then one would expect the same interpretation -- the physics of the moving observer with respect to the ether and the moving light source with respect to the ether would be understood like sound waves in air.
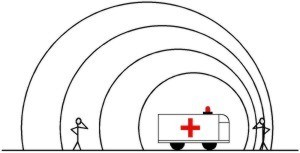 |
The siren's waves are
compressed as they enter the air in the direction of the vehicle's motion,
resulting in a higher pitch heard by the pedestrian, and stretched out
behind the vehicle, giving a lower pitch. In both cases the sound is
traveling at the same velocity with respect to the two observers. This
is different from the siren coming from a stationary vehicle, while the
observers move towards or away from it in cars. The observers would hear
higher and lower pitches, but the sound wave would be concentric circles in
the air, not stretched or compressed. With respect to the observers the
sound is traveling faster in one case, and slower in the other, than the
speed of sound in air. The change of pitch is the same for the moving
observer or moving source (the ambulance), but the physics is different.
|
Note: At the turn on the century there were many physicists proposing theories and ideas like the ideas in Einstein's 1905 paper. The notion that nothing could go faster that the speed of light and this limit would remake physics was proposed by the French mathematician Poincarre, and the very formula Einstein derives in special relativity had been derived by the Dutch physicist Lorentz based on the existence of ether. The idea that increased velocity would lead to increased mass, which is an assertion of Special Relativity, had been proposed (I can't remember by whom). Widespread acceptance of Einstein's version as to how it all fit together took many years...... Einstein's prominence in physics came not just from Relativity, but from the many answers he come up with, usually simple answers to problems that physicists around the world were trying to solve.
...............................................................................................................................................................................................................................
Now let's look at what is called a light clock, and look at one way the basic equation of special relativity can be derived based on the principle that the speed of light is constant in all moving frames of reference. By the reasoning described below, it is claimed that a clock moving at a high velocity will tick slower than a clock which is not moving. (A question this raises is: Why can't we say either clock is the non-moving one seen from the other clocks perspective, which would mean both clocks should slow down with respect to each other, which is impossible even in the strange world of Relativity. This is called the twin paradox, and it is dealt with differently by different physicists. One way is to introduce acceleration for one clock, making the clocks different. But a problem with this argument is that Special Relativity derives the slowing down of time for one clock without any acceleration. Furthermore different twin paradox arguments contradict each other. There are other aspects of Relativity which are not resolved to the agreement of physicists. For a web page on the twin paradox click here for Usenet Physics FAQ.
| In a light clock (see figure to right), a pulse of light (shown as a yellow ball) bounces up and down between two mirrors, as shown on the left (figure A). In figure B a light clock moves to the right so that, from the perspective of an observer who is standing still, the pulse travels farther in the same time than the pulse in the A light clock. Einstein's theory of relativity says this is impossible: one pulse light cannot travel faster than another pulse of light. From all vantage points (from every point of view), all light must travel at the same velocity, as described above (unless light enters a medium like water, which will slow it down). To compensate one may either adjust distance, or time, so that the speed of light may be considered constant. Special Relativity says time slows down. |
|
In the following sequence we show what happens if you work the math for the picture above based on the idea that light must have the same velocity in all perspectives. Rather than have two velocities, one for the light pulse in the A clock and one for the light pulse in the B clock, we have one velocity for the light pulses, but two options for time: time in the A clock's "frame of reference" and time in the B clock's frame of reference. We also show the math based on normal reasoning, with two velocities for the pulses and one time measurement for a pulse to bounce up and down. We show the normal math because it helps to clarify the difference between relativity and common sense geometry.
The figures and arguments below are representing the same concepts in the light clock figure above, just with more steps and more detail.
Below are two synchronized light clocks, shown on the left with the pulses going up, and shown on the right a moment later, after the pulses have reflected off the upper mirror and are headed back down. The light pulse is red, the black arrow just shows direction.
| Two light clocks in sync | The same clocks a moment later | ||
| >>>>>>>>> |  |
||
| figure 4a | figure 4b |
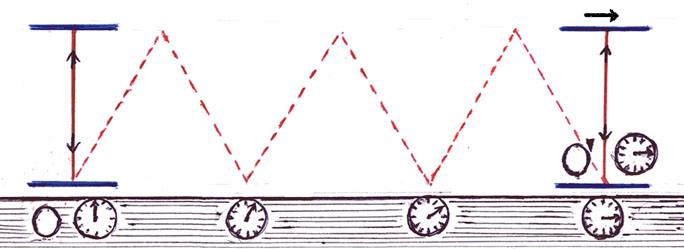
Below is a light clock on a railcar with a mechanical clock read by observer O' (which is read O prime). Observer O is on the platform with his mechanical clock synchronized with the mechanical clock of observer O. Imagine a second light clock right behind the first and synchronized with it, so that O and O' agree the two light clocks are in sync as measured by their mechanical clocks. Now (although this is impossible) imagine that the flatcar instantly moves to the right at a constant velocity. One light clock moves off with the flatcar, its ticks measured by O' and his mechanical clock. The other clock remains where it was, its ticks measured by O and his mechanical clock.
The dotted line below represents the path of the light pulse in moving light clock as "seen" from the ground. From O's perspective, which is the ground perspective, the pulse in the moving clock (on the flatcar) is traveling a longer distance for each tick than it travels from the perspective of the observer, O', on the flatcar. That means the light pulse is traveling faster in one frame than in the other. According to Einstein's special relativity this can't be so. The speed of light must be the same in all perspectives, all moving frames. He says that the light pulse in the moving clock moves at the same speed with respect to the ground as it does in the frame of the moving flatcar.
Special relativity says it is time that stretches to accommodate the constancy of the speed of light. In the arrangement below synchronized mechanical clocks are arrayed on the ground ( in the frame of observer O) beside the train, to record the ticks of the light clock on the moving train. O' has his mechanical clock and records the ticks of his light clock in his frame. Special relativity says the clock on the moving train will record a longer time for each tick of the light clock on than clocks on the ground will record for each tick of that same light clock. This means that a clock which takes a ride in space will come home registering less elapsed time than an identical, originally synchronized clock that stays behind.
 |
Before taking a closer look, a mathematical look, at why time must slow down in this way for Relativity to be correct, let's take a look at the common sense way of mathematically describing the diagonal path, h below, that describes the moving light-clock pulse from the ground perspective.
h, s and l (the letter "L" not the number 1) are distances -- a velocity multiplied by a time. ( for example 60 ft. = 10 ft. per second x 6 seconds)
By normal logic we would say:
In the ground frame the pulse (the pulse in the moving light clock) travels a longer distance (h) than the distance (l) that it travels in the frame of the moving light clock. Since this is the same pulse of light, the time for the pulse to make one "tick" in the light clock, that is, to travel from one mirror to the other, is the same from the stationary perspective and the perspective of an observer moving with the clock. So, since the pulse travels a longer distance as seen by a stationary observer than is does as seen by an observer moving with the light clock, we say that from the stationary perspective the pulse moves faster than it does as seen by the moving observer. This logic would lead to the definitions described and shown in the figure below.
| We define l, s, and h,
in the triangle above, as follows: l, the distance between the
mirrors, (the vertical path) equals C (the speed of light as measured by an observer and
source at a fixed distance from each other) times the time it takes for
one tick of the light clock, "delta" t. ("delta" the
triangle next to t for time is a Greek letter, used to indicate
"change in", meaning elapsed time in this case.) S,
(the black horizontal line) is the distance the
flatcar moves in one tick of the light clock. It equals the velocity of the
flatcar, V, times the time it takes for one tick of the light clock,
"delta" t. h, the diagonal line, is the distance traveled by the light pulse
in the ground frame. It equals an unknown velocity, faster than C, which
we call C', times the time for one tick of the time clock, "delta"
t.
|
|
As we show below (scroll down) this approach will give the mathematical result that C' is larger than C, as we would expect. In the ground perspective the pulse in the moving light clock travels a longer distance than it does in the frame of the flat car. The time interval, one tick of the light clock is the same for both paths. So the one velocity must be greater than the other.
..............................................................................................................................................................................................................................
| Let's go back to the h, s, l triangle, which we have just defined above based on the common sense argument that the light pulse in the moving light clock moves faster, as seen by a stationary observer, than it moves as seen by an observer moving with the light clock. (This triangle, remember, represents distances. h is the distance traveled by a light pulse as seen by a stationary observer. l is the distance traveled by a light pulse as seen by an observer moving with the light clock, which is the same as for a stationary observer and a stationary clock.) Now we define h and l based on Einstein's assumption that there cannot be a C and a C' as we wrote above. There can only be one speed for the light pulse in the light clock no matter the perspective. Whether one is moving with the moving light clock, or on the ground watching it go by, the speed of light is the same. Bear in mind that this does not make any sense, and there seems to be no reason to make such a nonsensical assumption. It is hard to wade into the thinking of Special Relativity because there is no physical reason to prompt us to say that the speed of light is constant in all moving frames. Special Relativity is illogical. |
Given, then, that the speed of light is the same in all moving frames, to all observers, the light pulse must have the same velocity with respect to the ground frame observer as it has with respect to the observer moving with the light clock. How can this be? It can be if we say h = l, so that h divided by the time for one tick of the light clock will be the same as l divided by the time for one tick of the light clock, yielding the same velocity. However, to say h = l, that the distance the light pulse travels seen from the ground frame is the same as the distance the light pulse travels seen from the moving frame, is a tough pill to swallow. If we accept that h is a longer distance than l, how can h divided by time give the same velocity as as l divided by time -- where the time in question is one tick of the light clock? We can get that result by defining two time intervals for a tick of the light clock, one measured by the moving observer, and one as measured by the stationary observer. Since h is a larger distance than l, to get the velocities the same, h must be divided by a time interval that is longer than the time interval by which l is divided. This way h divided by time(in stationary perspective) = l divided by time (in moving perspective). Or, h / t (stationary perspective) = l / t (moving perspective)
In other words, to get the desired (illogical) result, that the velocity of the light pulse is the same for the stationary and moving observer, we must say that a tick of the moving light clock takes longer as measured by the stationary observer than is does as measured by the moving observer. Below we rewrite the l s h triangle so the speed of light is the same for the moving and the stationary observer.
| According to special relativity l, s and h, (from the triangle, scroll up) are defined as follows: l, the distance between the mirrors of the light clock, is the same as simple logic would define it -- the speed of light, C, times the elapsed time for one tick of the light clock, "delta" t. S equals the velocity of the flatcar (the velocity of the moving time clock) times an unknown elapsed time, "delta" t' which is the time it takes for one tick of the moving light clock according to an observer in the ground frame. h equals the velocity of light, (the same as for the pulse in the light clock) times the same unknown elapsed time, "delta" t'. |
|
The math for the light clock, by normal logic and according to relativity are shown below. By normal logic the velocity of the pulse of light in the moving light clock, according to the stationary observer, is the unknown. So we solve for that velocity, C'. as shown in the left frame below. The result is, as expected, that C' is greater than C. The first term is according to the Pythagorean theorem. (C' is greater than C because the square root of C squared is C, whereas the square root of V squared plus C squared is greater than C.)
According to special relativity, the time for a tick of the moving light clock according to the stationary observer is the unknown, so we solve for that, "delta" t', as shown below, right. The solution says that as V, the velocity of the light clock, increases, time slows down for that light clock and mechanical clock, as compared with clocks in the stationary frame.
| As would be expected by common sense, C', the velocity of the light pulse in the moving light clock as measured by the stationary observer, is greater than the velocity of the light pulse measured by an observer moving along with the light clock. | The last term is the basic equation of Special Relativity. As V, the velocity of the light clock increases, the light clock will tick slower. |
Question cited above: An immediate objection to the thinking outlined above is as follows: From the point of view of the "moving" observer it is the other observer who moves. If the two are in space, one is no different from the other. If we call them A and B, we can say A is stationary and thus B's clock slows down. But we can say with equal validity that B is stationary and A's clock slows down. The two clocks cannot go slower than each other. To address this dilemma some argue that the difference between the two clocks is that one accelerates, while the other does not. We would like to describe and compare the various approaches to resolving the "twin paradox." For a discussion of the twin paradox .... click here for Usenet Physics FAQ. This gets really tricky because there are a variety of views as to how the "twin paradox" should be resolved, and they are not in agreement.
Here is a another question would like to discuss: (The following question requires an understanding of the Michelson-Morley experiment, which we will discuss here, on this page when we get to it --soon. Look it up on the Web, please, for now.) Is there anything wrong with the Michelson-Morley result, once we accept there is no ether? If so what? It would seem there is no reason to invoke the idea of C being constant in all moving frames, as textbooks do, to explain M.M. Without ether the result is intuitively correct. The apparatus is standing still, in physics terms -- it is an inertial frame, as it is treated in textbook arguments. As with ignoring friction in a problem "mechanics" problem, we are told to in textbook arguments to ignore the acceleration effects of the earth turning and the earth orbiting the sun. This is the same as saying that the M.M. apparatus is out in space, not accelerating. Its tangential velocity is all we are supposed to take into account -- but that only has meaning with respect to the ether, which we have decided does not exist. Given these assumptions, there is nothing to cause a discrepancy in the split light paths, is there? Furthermore, M.M. is contained in one inertial frame. So why invoke the issue of different moving frames -- special relativity -- to explain an experiment that is all in one inertial frame? (There is a version of M.M. using starlight, but that is not the one they use in textbooks.) The issue of the velocity of light being independent of the velocity of the source of the light has no meaning when the source and observer are effectively standing still (an inertial frame).
................................................................................................................................................................................................................
back to Stopdown, home page, click here
back to Science, home page, click here
It is said in physics texts that the dilemma of the Michelson-Morley experiment (1887), was resolved by Einstein when he dispelled the ether and stated that the speed of light is constant in all moving frames.(1905) We would like to raise two questions about this standard text presentation of special relativity.
(1) The Michelson-Morley result surprised scientists because the effect of the ether on the light pathways, like the effect of a current on a swimmer, was not observed. We ask this: except for the ether, was there, is there, anything wrong with the Michelson-Morley result? If so, what? That the split light beams should go out and come back without any distortion is to be expected, is it not, in an inertial frame? (The M/M apparatus is an inertial frame, correct?)
It would seem that by dispelling the ether, Einstein resolved the problem. So why is the special relativity principle, that C=c in all moving frames, invoked here when the problem is resolved?
(2) The Michelson-Morley apparatus is in an inertial frame, one frame. Special relativity refers to different moving frames, so why is it invoked when it does not apply? There is a version of the experiment in which starlight, rather than an internal source, is used, and in that case Special Relativity is pertinent. But in the texts the light source is in the same inertial frame
Below is another representation of a binary star. "Red" and "Blue" refer to redshift, meaning a change in wavelength towards the longer wavelength end of the visible spectrum, and blueshift, meaning a shift to the shorter wavelengths of blue light. (Beyond blue and red are ultraviolet and infrared, which we can't see.) The equivalent of blueshift and redshift in sound is the trainwhistle pitch going from high to low as the train comes towards you and then moves away.
|
||||||
...lkfdjskfdfds
In the figure below, star 1 and star 2 circle each other, connected by gravity, in what is called a binary star. The three arrows closer to the binary star show how one might picture the light coming off of this system, if one assumed that the motion of the source of light changed the velocity of light originating from that source. At the top of the orbit star 1 is moving towards the observer, at its orbital velocity V, emitting light at the combined velocity of C+V. At the next position it is moving down, meaning it is not headed away from or towards the observer, so its light's velocity is just C. When it reaches the bottom of the circle star 1 is headed directly away from the observer, its light's velocity in the observers frame should be C - V. If the light's velocity, with respect to the observer ( who is not moving with repect to the center of this binary system) changed according to the source's motion, the image in the observer's telescope would be confused. The light from the top of the orbit would reach the observer ahead of light from the bottom of the orbit. In fact a binary star in a telescope looks as is should, meaning that the second set of arrows, with light from all points on the orbit traveling at the same velocity, C, represents what happens in nature. The terms of special relativity fit with what the binary star shows us. (It may be noted that under the "ether" hypothesis light waves from differently moving sources would travel at the same velocity, with respect to the ether, as do soundwaves with respect to the air. So the intact binary star image would be expected under the ether hypothesis.)
 |
Figure 3 below is a depiction of an Einstein "thought experiment" that describes how simultaneous events may be perceived. In the top image a train is moving past a platform, pictured at the moment observer O', on the train, and observer O, on the platform, are "coincident", i.e. lined up opposite each other. At that same instant two flashes of light occur, at points C1 and C2 on the platform, which are directly across from points C1' and C2' on the train. In the bottom image the train has moved a distance as shown. Since O' is closer to the C2 flash he will see it before he sees the flash from C1, whereas O will see the flashes at the same time. Conversely, if the left flash occurs before the right flash in the platfom frame, and if the timing is just right, the flashes will reach O' at the same time.
So far common sense is intact. Gallileo and Newton would agree that light signals could deceive an observer because of relative motion between light source and observer. But at this point Einstein declares that simultaneous events can only be defined by the arrival of two light signals at the same time, and that there is no abstract conception of distance and time that can define simultaneous events. In the case we described above, where two light flashes were emitted at different times but the observer's motion gave him the impression they were emitted at the same time, Einstein claims the events were simultaneous since their signals arrived at the same time. This definition of simultaneity is, like the assertion that the speed of light is the same in all moving frames, quite illogical.
| figure 3 ......Simultaneous flashes are ignited at C1 and C2, on the platform, making marks at C1' and C2', on the train. |
hajshd
| figure 4 | ...The top and bottom events are the same event, seen from two perpectives. |
ldklskfdjlkdf
jlaksdjalksda
lkdjskdjlskdfjkfd
Suppose the light sources are moving with respect to the observer as in figure 2 above. The standard simultaneity definition here is more slippery because we don't know if the velocity of the source changes the velocity of the light pulse. Since the flashes are, according to special relativity, expected to arrive at O at the same velocity, this would mean the velocity of the source is not imparted to the light flash, and one would expect the flashes to reach O at the same time. And, in fact, light from a pair of spinning stars (called a binary star) reaches earth with a coherent image, which supports the same-time argument in the case of figure 2. (Click here for a discussion of binary star and relativity.)