
Electron Orbitals and the Electron's Wave Nature
This page looks at electron orbitals, the spaces to which electrons are confined as they circle the atom. The reason for these confinements cannot be understood unless one looks at the wave nature of electrons, which raises the issue of the wave-particle duality. This concept is not hard to grasp if one looks at what waves do when they make an interference pattern, and then one looks at how particles, small particles like electrons and protons which are moving fast, turn into waves.
This phenomenon is observed in biochemistry where enzymes, proteins which speed up reactions, invite electrons and protons from the reactants to shift to their wave nature so that the reaction can proceed much faster than if the electrons and protons remained as particles. We don't have a page on this yet, but do a Google search on this: enzymes, quantum tunneling, and you will find articles of varying difficulty.
..............................................................................................................................................................................................................................
Physicist Neils Bohr determined that light comes from electrons when they drop from an "orbital", a sort of flight pattern around the nucleus, to another orbital closer to the nucleus. But the question as to why electrons were stuck in orbitals remained unanswered in the early 1920's.
| Louis de Broglie, while a university student, mused that if light had a particle nature, as Einstein had argued, then particles might have a wave nature. He published his idea in 1924...... The most graphic experiment with particles behaving like waves involves shooting particles, such as electrons or protons, at a screen with two slits allowing the particles to pass through and travel on to hit a screen which is a detector. The pattern on the screen turns out to be an interference pattern such as waves should make. What exactly is going on here remains unexplained. Particles fired one by one, still give a wave like interference pattern over time. One problem it that when scientists try to look at the event from the side, to see what slits the particles are emerging from and what is going on, it stops happening. The particles behave as particles, making two bands on the screen instead of a wave-like interference pattern (and no one denies that this is REALLY weird, as if the particles know they are being observed and are refusing to perform.).... De Broglie did not have the benefit of this experiment, which came later. |
 |
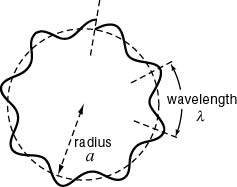
De Broglie's idea led to an understanding of why electrons are restrained to orbitals. If an electron has a wave nature, then its wavelength should fit into the orbit of the electron so that a "standing wave" is possible, the meaning of which can be best understood by comparison with a guitar string. The basic idea is that the orbit of the electron will be an "integral" number of wavelengths, one, two, three....ten, but not one and a half, or five and one third, or any such number that is not a whole number. (See images below.)
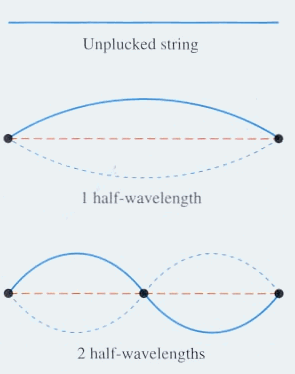
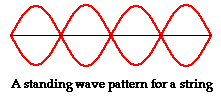
A guitar string resonates at a given pitch because fixed numbers of wavelengths become established between the point where the finger holds the string down and the "bridge" of the guitar. If there were fractions of wavelengths running back and forth no particular pitch would result. As nature would have it, the string resonates at its simplest state, n=1, and then its "overtones", n=2 etc.
In the case of the electron, its wave nature also seeks this orderly condition, with an integral number of wavelengths fitting into the orbit, no fractions left over. As to why this should be, it is said that with fractions of wavelengths the electron's wave nature would interfere with itself. If the electron wave ends where it began, then there is a "standing wave" and no interference.
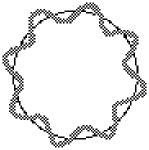
To the left, below, is shown how waves not fitting the orbital results in the wave interfering with itself. The standing wave cannot become established. On the right is an image of the waves fitting the orbital, with no interference, so that a "standing wave" can exist. To picture a standing wave in action, imagine the curves inside the circle going outside at the same time as the outside curves go inside, so it is flip flopping. Scroll down a little for standing wave images better illustrate this action.
 |
 |
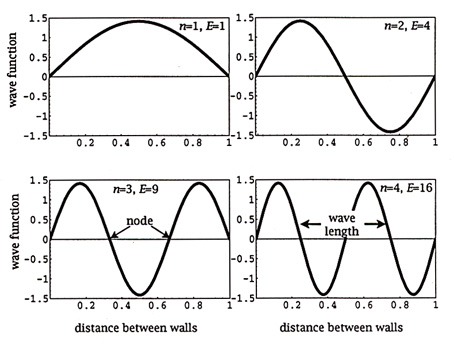
The images below show standing waves as on a guitar or violin string, a straight line arrangement rather than circular as above. The same principle is at work -- the waves that fit the space make a standing wave, avoiding the conflicting energies of overlapping waves. The waves are happiest this way, it may be said. When physicists speak of the particle in a box, which bounces between two walls, they are talking about an electron bound to its orbital by its wave function. If the electron starts to move out of this orbital its wave aspect starts to interfere with itself, driving it back into the orbital where a standing wave is formed and there is not interference. The box image is like the guitar image, linear rather than circular.
 |
 |
For an animated version of a standing wave, click here.
The article below addresses "quantum tunneling", in which electrons, protons, and atoms in reacting chemicals take on their wave nature to facilitate the reaction. Usually two reacting molecules must collide with enough energy to overcome the reaction energy barrier. That is the classical picture of a chemical reaction, and in most cases that is what is going on.
|
Science, Feb 7, 2003 v299 i5608 p833(2)
Full Text: COPYRIGHT 2003 American Association for the Advancement of Science. Understanding chemical reaction rates constitutes a central theme in chemistry. Classical theories have been tremendously successful in providing qualitative and quantitative insights into chemical reaction rates. Yet, a growing and remarkably varied number of chemical reactions deviate from classical behavior because of quantum effects (1). As Zuev et al. show on page 867 of this issue, these deviations can be enormous (2). Far from being mere curiosities or footnotes in the theory of chemical reaction rates, these quantum phenomena manifest themselves in "ordinary" chemical reactions (see the first figure) (1-8), with important implications for chemical catalysis (9), enzymology (10-13), and interstellar chemistry (14). Zuev et al. present a stunning example of a reaction in which heavy-atom tunneling of carbon affords a rate enhancement of 152 orders of magnitude over the rate expected without tunneling (2). Tunneling in chemical reactions arises from wave-particle duality. The "panicle in a box" problem tells us that the probability of finding the panicle inside the box is unity only when the potential barrier for the walls of the box is infinitely high (see the second figure). For a finite potential barrier, the wave function penetrates the barrier wall, and there is a finite probability of finding the particle outside the box. Applying this qualitative picture to a potential-energy diagram for a chemical reaction involving proton transfer, we see that the wave function describing the O-H stretching vibration penetrates the barrier wall. There is a finite probability of finding the proton on the other side of the potential barrier, regardless of whether or not the system possesses sufficient thermal energy to surmount the activation barrier. There may thus be competing pathways for a chemical reaction: a classical process (over the barrier) and a quantum mechanical process (through the barrier). The quantum mechanical process is called "tunneling." Contrary to expectation, the barrier width (the distance the nuclei move in passing through the barrier) is more crucial than the barrier height in controlling the tunneling reaction rate.
The manifestation of wavelike properties is inversely related to the mass of the panicle. The electron's small mass confers a large de Broglie wavelength, which means that wavelike properties (tunneling) manifest themselves on a length scale that is large compared to the dimensions of molecular chemical systems. Thus, electron tunneling occurs throughout chemistry and forms the physical basis for scanning tunneling microscopy (STM). The proton ([H.sup.+]), hydrogen atom ([H.sup.*]), and hydride ion ([H.sup.-]) are much more massive than the electron, and have smaller de Broglie wavelengths. Nevertheless, their de Broglie wavelengths are similar in dimension to the distance involved in common chemical reactions such as proton transfers between bases. Tunneling by hydrogen species is of central relevance to acid-base reactions, atom transfer reactions of various organic reactive species, and conformational inversion of amines and radicals (1, 15) (see the first figure). Hydrogen tunneling also occurs in redox enzymes (10-13) and in proton-coupled electron transfer reactions (16). Chemical reactions involving tunneling by atoms heavier than hydrogen are rare. Even those that are known are not widely appreciated. In the first figure, the second and the last five examples involve heavy-atom tunneling. Nuclear motion by several heavy atoms may be involved. Experimental evidence for tunneling comes from kinetic or spectroscopic measurements. The simplest description of classical kinetic behavior is the Arrhenius equation (1) k = A exp(-[E.sub.a]/RT) where k is the rate constant, A is the Arrhenius preexponential value, Ea is the activation energy, R is the universal gas constant, and T is the temperature. Deviations from classical behavior may show up as a nonlinear Arrhenius plot, a low-temperature regime in which the reaction rate is independent of temperature, anomalous values of A, an unusual kinetic isotope effect, or a reaction rate that is faster than expected. Spectroscopic observation of a tunneling splitting in the Raman or microwave spectrum, as in the classic case of ammonia inversion (see the first reaction, first figure), represents unambiguous evidence for tunneling. A key feature that differentiates classical and tunneling pathways is the temperature dependence of the rate. The classical component is a thermally activated process and displays a strong temperature dependence (Eq. 1). In contrast, the tunneling rate is to a first approximation temperature independent. Many examples of tunneling derive from kinetic measurements at cryogenic temperatures, where the thermally activated rate becomes negligibly slow and the tunneling pathway dominates (15). A common misconception, however, is that tunneling is important only at cryogenic temperatures. It is now well established that tunneling contributions may be substantial at room temperature and under physiological conditions. The strong dependence of tunneling rate on distance (that is, barrier width) creates two interesting scenarios in which the tunneling rate may be convoluted with a thermally activated process. Thermal population of higher vibrational levels may lead to a faster tunneling rate because the barrier effectively "narrows" as one moves up from the bottom of the potential-energy well. Large-amplitude conformational motions that bring reacting centers in close proximity may also promote tunneling. Zuev et al. report a stunning example of heavy-atom tunneling (2). They monitored the kinetics of the rearrangement of the reactive carbene 2b to cyclopentene 3b (see the first figure) by infrared spectroscopy in a frozen nitrogen matrix at 10 K. Electronic structure calculations predict a barrier of 27 kJ/mol for this rearrangement, implying that the rate of the classical (thermally activated) reaction will be vanishingly small at 10 K; in effect, the reaction should not occur. Calculations incorporating the effects of multidimensional tunneling reveal that the rearrangement reaction occurs by carbon tunneling from the lowest vibrational quantum state. The computed tunneling rate is consistent with the experimentally measured rate. The rate enhancement of the carbon tunneling versus the classical pathway is a factor of [10.sup.152]. The synergy of theory and experiment in the current study affords tree insight. The development of reaction dynamics calculations that include tunneling dramatically enhances our ability to understand and interpret tunneling phenomena in chemistry. The current investigation opens a new chapter in the study of heavy-atom tunneling in chemical reactions.
References (1.) R. P. Bell, The Tunnel Effect in Chemistry (Chapman & Hall, New York, 1980). (2.) P. S. Zuev et al., Science 299, 867 (2003). (3.) G. Brunton, D. Griller, L. R. C. Barclay, K. U. Ingold, J. Am. Chem. Soc. 98, 6803 (1976). (4.) D. J. Miller, R. Subramanian, W. H. Saunders Jr., J. Am. Chem. Soc. 103, 3519 (1981). (5.) S. L. Buchwalter, G. L. Closs, J. Am. Chem. Soc. 101, 4688 (1979). (6.) H. Frei, G. C. Pimentel, J. Phys. Chem. 85, 3355 (1981). (7.) B. K. Carpenter, J. Am. Chem. Soc. 105, 1700 (1983). (8.) F. L. Bettens, R. P.A. Bettens, R. D. Brown, P. D. Godfrey, J. Am. Chem. Soc 122, 5856 (2000). (9.) S. E. Wonchoba, W.-P. Hu, D. G. Truhlar, Phys. Rev. B 51, 9985 (1995). (10.) M. J. Knapp, J. P. Klinman, Eur. J. Biochem. 269, 3113 (2002). (11.) S. Hammes-Schiffer, Biochemistry 41, 13335 (2002). (12.) D. Antoniou, S. Caratzoulas, C. Kalyanaraman, J. S. Mincer, S. D. Schwartz, Eur. J. Biochem. 269, 3103 (2002). (13.) J. Gao, D. G. Truhlar, Ann. Rev. Phys. Chem. 53, 457 (2002). (14.) K. Hiraoka, T. Sato, T. Takayama, Science 292, 869 (2001). (15.) V. A. Benderskii, D. E. Makarov, C. A. Wight, Adv. Chem. Phys. 88, 1 (1994). (16.) S. Hammes-Schiffer, Acc. Chem. Res. 34, 273 (2001).
The author is in the Department of Chemistry, University of Wisconsin, Madison, WI 53706, USA. E-mail: mcmahon@ chem.wisc.edu |
||||||
Article A98469664 |
||||||