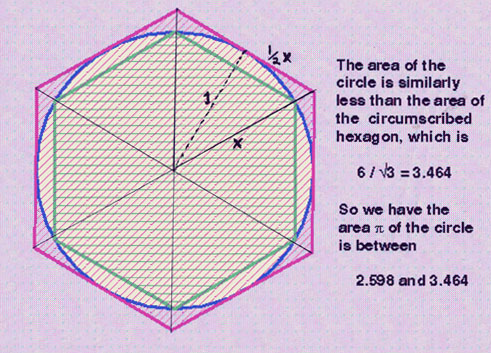
Here is the calculation for the area of the outer hexagon.
| Again we need to find the area of an equilateral triangle, this time we know that the height of the triangle equals one, the radius of the circle, as we show in black. (It is quite remiss of the authors just to state the area, without showing the math, we think) But we need to find X in the diagram. Since X is the hypotenuse of a right triangle whose legs are 1 and 1/2 X, by the Pythagorean theorem we have 1 squared plus (1/2 X) squared = X squared. So X squared minus 1/4 X squared = 1. So 3/4 X squared = 1. Thus, X squared = 4/3 and X = 2 / the square root of 3......The area of the equilateral triangle is one half the base times the height. The base is X ( 2 times 1/2 X...pink line, not black), the height is 1. The area is 1/2 times (2 / the square root of 3) times 1 which equals 1 / the square root of 3. Since the hexagon consists of six such triangles, the area of the hexagon is 6 times (1 / the square root of three) which is 6 / the square root of three. |  |