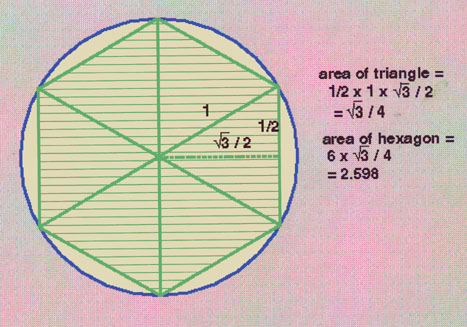
To calculate pi the area of a hexagon inscribed in a circle is calculated, and this is compared with the area of a hexagon framing the circle, as shown in the next step. The area of the circle must lie between these two areas. Pi can be approximated from this approximated area.

*  The triangle whose area is being calculated is one of the six equilateral triangles.  (We are not sure how you prove that a hexagon so divided makes six equilateral triangles, but would like to know) (An equilateral triangle is one in which the three sides and the three angles are equal.) The dotted line is the "height", the base is the side bisected by the dotted line. The area of a triangle is "one half the base times the height." So the base is 1, and the "height", shown as the square root of 3 divided by two, is determined by the Pythagorean theorem. The height, call it x, (the dotted line) is a leg of the right triangle with 1/2 as the the other leg (half of one of the sides of the equilateral triangle whose sides = 1) and a hypotenuse of 1. By the Pythagorean theorem: 1/2 squared plus x squared = 1 squared. By algebra we get x squared = 1 minus 1/4, so x = the square root of 3/4 which is the square root of 3 divided by 2. The area of the triangle and the hexagon  can be calculated as shown on the slide.